El Teorema de los Números Primos

Ya que estamos en el tema de losnúmeros primos, no puedo dejar de comentar sobre el teorema de los números primos. En su forma más sencilla, este notable teorema dice que la cantidad $pi(x)$ de primos menores o iguales que un número $x$, es aproximadamente $x/log(x)$ cuando $x$ es grande, simbólicamente

Para ser más precisos: esta relación dice que el cociente entre ambas cantidades tiende a uno cuando $x$ tiende a infinito).

Cuando me enteré por primera vez de la existencia de este teorema (leyendo el hermoso libro de R. Courant y H. Robbins “¿Qué es la Matemática?”) me sorprendió mucho: ¿pues acaso qué tienen que ver los números primos con el logaritmo (natural) ? A primera vista, uno podría pensar que nada, y sin embargo este teorema muestra que existe una profunda conexión entre ambos conceptos: la función logaritmo permite describir la distribución de los números primos.

Como comenté en el post anterior, la historia de este teorema es fascinante. Fue incialmente conjeturado por Legendre (hacia 1797) y Gauss (hacia 1792). Una aproximación aún más precisa está dada por la función logaritmo integral

lo que fue propuesto en Dirichlet en 1838. Pero ninguno de estos grander matemáticos logró demostrarlo.

El siguiente gráfico realizado con SageMath permite comparar la bondad de esta aproximación. En azul, aparece la función $\pi(x)$ que cuenta los primos. En rojo, la función $x/log(x)$ que la aproxima. En verde, la función logaritmo integral $\text{Li}(x)$ que como dijimos, da una aproximación más precisa.

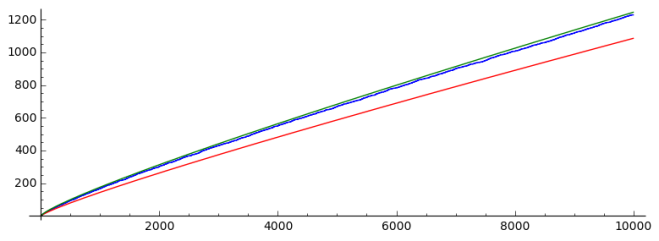
El código en SageMath que usé para generarlo es:

Azul=plot(prime_pi, 2,10000, rgbcolor="blue")
Rojo=plot(x/log(x), 2,10000, rgbcolor="red")
Verde=plot(Li(x), 2,10000, rgbcolor="green")
show(Azul+Rojo+Verde,xmin=0,figsize=[8,3],filename="/home/pablo/pnt.png")

Un primer avance fue realizado por el matemático ruso Pafnuti Chebyshov (1848 - 1850), quien demostró que $x/log(x)$ era el orden de magnitud correcto de  $\pi(x)$, y que el límite del cociente entre ambas cantidades si existía, tenía que ser 1. Pero no logró demostrar que dicho límite existiera.

Más tarde,  en 1859, el matemático alemán Bernhard Riemann  publicó su célebre trabajo donde introdujo las ideas fundamentales que permitieron demostrarlo. En él, Riemann introduce la función zeta , la estudia por los métodos del análisis complejo (una rama de la matemática que él mismo con éste y otros trabajos contribuyó mucho a desarrollar), la relaciona con la distribución de los primos y formula la célebre hipótesis de Riemann (unos de los problemas abiertos más importantes de la matemática actual). Otros aspectos notables del trabajo de Riemann son que tiene sólo unas diez páginas y es el único artículo de Riemann dedicado a la teoría de números en toda su vida.

Pero hubo que esperar 37 años para que el análisis complejo se desarrollara lo suficiente, y entonces siguiendo las ideas de Riemann, finalmente en 1896,  Jacques Hadamard y Charles Jean de la Vallée-Poussin lograron (independientemente) dar demostraciones completamente rigurosa del teorema de los números primos.

Posteriormente, se dieron varias demostraciones alternativas. Creo que la más sencilla es la de Donald J. Newman que no requiere usar mucho más análisis complejo que el teorema de la integral de Cauchy. Aquí el artículo original. También pueden encontrar una exposición detallada en el execelente libro de Análsis complejo de R. Ash y W.P. Novinger.

También en 1949, Atle Selberg y Paul Erdős lograron dar pruebas elementales de este teorema, que no dependen de la teoría de la función zeta de Riemann. Pero honestamente, este tipo de pruebas son mucho más difíciles de seguir, mucho más oscuras, que la demostración analítica (que está al alcance de cualquiera que haya pasado por un curso de análisis complejo). Existe también una prueba basada en el teorema tauberiano de Wiener.

Si les interesó el tema, pueden encontrar varias referencias relacionadas, en la página de un curso de teoría analítica de números que di en 2009.