¿Cuál es la probabilidad de empate en un balotaje ?

Hoy es día de elecciones en Argentina, y esto me ha motivado a plantear un problema matemático que quiero compartirles. Este problema consiste en estimar la probabilidad de empate en un balotaje. Su solución involucra varios conceptos centrales de la teoría de probabilidades. Pero desarrollarlo, resultó bastante largo. Por lo que voy a dividir el artículo en varias partes. Espero que lo disfruten.

Introducción ¿Qué es el balotaje?

La Constitución Nacional, tras su reforma de 1994 , establecío (en sus artículos 94 y 96) el sistema de segunda vuelta electoral o balotaje, en reemplazo del sistema de Colegio Electoral que había regido hasta entonces.

En esta segunda vuelta se enfrentan las dos fórmulas más votadas en la primera vuelta (salvo que se cumplan algunas de las condiciones establecidas por los artículos 97 y 98). En consecuencia, cada elector se enfrenta a tres posiblidades: votar por alguno de estos dos candidatos, o votar en blanco. (No ir a votar o anular el voto a los fines de este artículo, equivalen a votar en blanco.)

Esta situación naturalmente plantea la siguiente pregunta: ¿cuál es la probabilidad de que haya un empate en el balotaje? (situación para la cuál la Constitución Nacional no prevé una solución) o lo que es virtualmente equivalente ¿Cuál es la probabilidad de que la elección termine definiéndose por un sólo voto?

Intuitivamente, esto depende de la cantidad de electores, que llamaremos $n$. Cuanto más grande sea $n$, menores serán estas probabilidades. Dado que en Argentina, hay actualmente 35.394.425 electores habilitados para votar, uno imagina que esta probabilidad es realmente muy pequeña. Que es un evento virtualmente imposible en términos estadísticos.

¿Pero cómo podemos cuantificarlo? Ahí es donde la matemática, y en particular el cálculo de probabilidades viene en nuestra ayuda.

El problema del empate si no hubiera votos en blanco

Como toda situación en la que queremos aplicar la matemática a un problema real, debemos hacer una modelización del problema. Es decir, representarlo por medio de ciertos objetos matemáticos. Esto siempre introduce algunas suposiciones y simplificaciones en el problema, que dependiendo de la situación pueden ser más o menos realistas o cuestionables.

Una cosa que los matemáticos solemos hacer es analizar primero una situación más simple. Entonces vamos a empezar suponiendo que no hubiera votos en blanco. Si hay $n$ electores, para que hubiera un empate tendría que haber entonces exactamente $n/2$ votos a uno de los candidatos (y $n$ tendría que ser un número par).

En las encuestas electorales se suele utilizar el siguiente modelo probabilístico. Supongamos que uno de los candidatos (llamémoslo A) tiene una cierta intención de voto $p$ (medida por una probabilidad, que es un número entre $0$ y $1$, que representa que fracción de los electores está dispuesto a votarlo), el otro candidato (llamémoslo B) tendrá entonces la probabilidad $1-p$. Y si suponemos que los electores votan en forma independiente uno de otros (suposición que podríamos cuestionar, pero que como les digo es necesaria para poder hacer un modelo matemático), entonces podemos pensar que estamos en una situación donde se realizan $n$ ensayos de Bernoulli con una probabilidad de ”éxito” $p$. Obviamente, a priori no conocemos $p$, pero podríamos estimarlo por medio de una encuesta. Gran tema para otro artículo, otro día.

Entonces, la cantidad de votos que recibe uno de los candidatos es una variable aleatoria que tiene distribución binomial distribución binomial. Con lo cuál, la probabilidad de que valga exactamente $n/2$ viene dada por la función de probabilidad puntual de dicha distribución evaluada en $n/2$, o sea:

Acá estoy usando el nombre que esta función tiene en Scipy, la biblioteca de python que utilicé para realizar el siguiente programita que muesta el gráfico de esta probabilidad como función de $p$ para distintos valores de $n$:

import numpy as np
from scipy.stats import binom
import matplotlib.pyplot as plt
p=np.linspace(0,1,num=1000)

def graficar_probabilidad_de_empate(n):
    empate= binom.pmf(n/2,n,p)
    plt.plot(p,empate,label="n="+str(n))

graficar_probabilidad_de_empate(100)
graficar_probabilidad_de_empate(200)
graficar_probabilidad_de_empate(300)

plt.legend()
plt.grid()

Acá pueden ver el gráfico resultante:

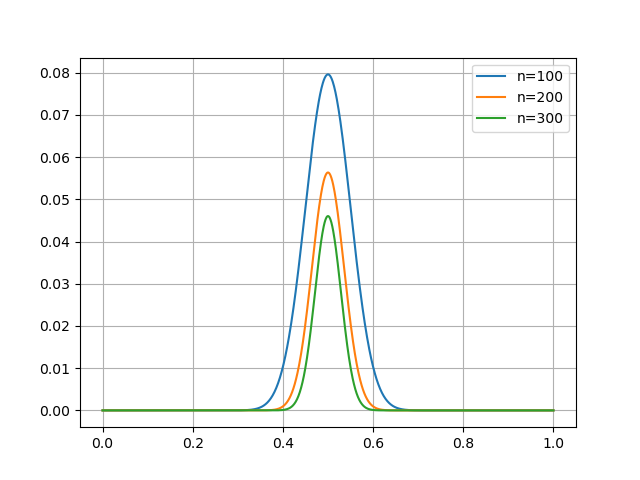
Este gráfico nos permite sacar algunas conclusiones, que son intuitivamente razonables:

• La probabilidad de empate es máxima cuando $p=1/2$, o sea cuando la elección está tan peleada que ambos candidatos tienen un 50% de intención de voto. Disminuye rápidamente cuando nos alejamos de ese escenario.

• Esta probabilidad máxima de empate también disminuye cuanto mayor es el número $n$ de electores. Con $n=300$, vemos que ya hay apenas un $8\%$ de probabilidad de empate.

Sin embargo, aún nos queda el problema de estimar esta probabilidad en función de $n$ para entender cómo es esta dependencia (y en particular ¿qué pasa cuando $n=35394425$ ?). Este problema lo abordaremos en la segunda parte del artículo, y no se la pierdan ¡Porque sorpredentemente el número $\pi$ aparece en ella !.

Si pasaron por un curso de probabilidades, la respuesta será quizás obvia a esta altura, pero si no se preguntarán ¿qué tiene que ver la longitud del cículo con la probabilidad de empate en le balotaje?. Otra muestra de la sorprendente unidad de la matemática …